从神经元到神经网络

  神经网络（neural networks)方面的研究很早就已经出现，今天“神经网络”已经是一个相当大的，多学科交叉的学科领域。神经网络已经出现了很多种类，比如CNN(Convolution Neural Network), RNN(Recurrent Neural Network)等等。下面将从神经网络的最基础的模型神经元逐步深入到CNN， RNN。

什么是神经元（neuron)?

  神经元是神经网络中最基本的成分。在生物神经网络中，每个神经元与其他神经元相连，当它“兴奋”时，就会向其他神经元发送化学物质，依次改变神经元内的电位。如果神经元内的电位超过某一个阈值(threshold)，那么它就会被“激活”为“兴奋”状态，继续为其他神经元发送化学物质。
  神经网络的灵感就来源于生物神经网络，即它接受一些输入，然后给出一个输出。在机器学习中，神经网络就是一个数学占位符，它的工作就是对输入进行一个函数变换，然后给出输出。

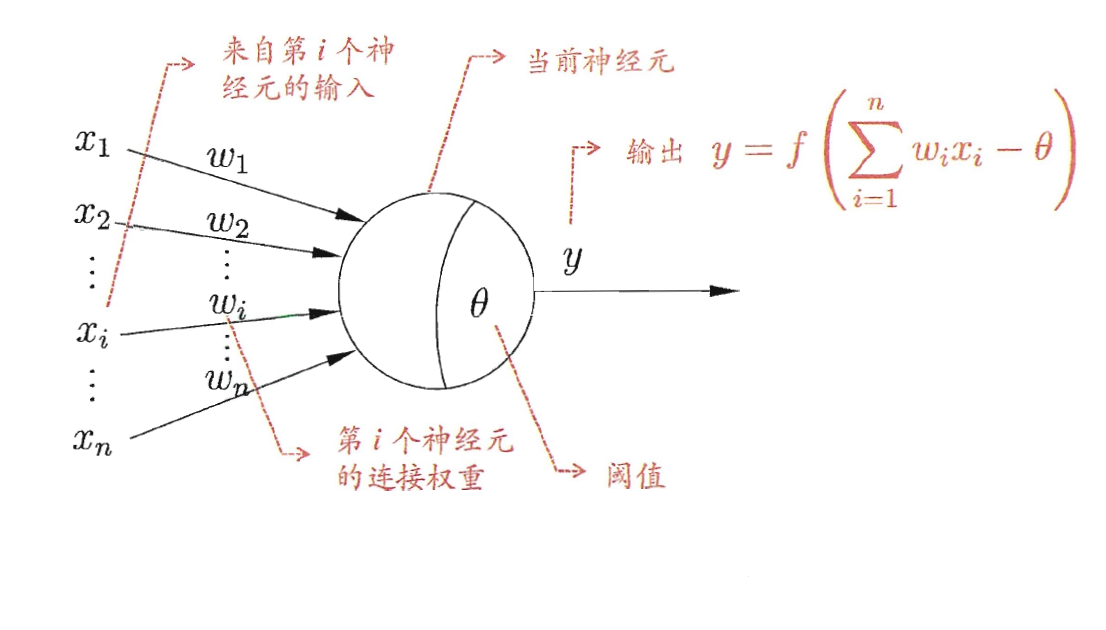
  在神经元模型中，该神经元收到来自其他n个神经元的通过带权连接传递的输入信号。神经元要将接受到的总输入值与神经元的阈值进行比较，然后利用激活函数(activation function)进行变换产生神经元的输出。

常见的激活函数

阶跃函数(step function)

  阶跃函数是最理想的激活函数，因为它将输入值映射为“0”或者“1”，分别对应神经元的“抑制”或者“兴奋”。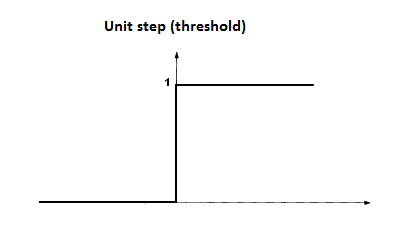

$$sgn(x)=\begin{cases} 1,\quad x\geq 0 \\\\ 0,\quad x<0 \end{cases}$$

  但是在实际应用中阶跃函数由于其不连续、不光滑的数学性质不常被使用。

Sigmoid函数

  典型的Sigmoid函数如下图所示：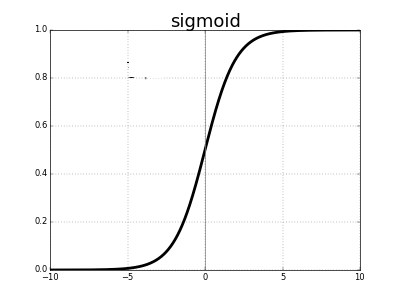

$$sigmoid(x)=\frac{1}{1+e^{-x}}$$

  Sigmoid函数可以把较大范围内变化的输入值挤压到（0，1）范围内，因此有时也被称为挤压函数， 它适合输出为概率（但是不等同于概率）的情况。
利用Sigmoid函数最为激活函数主要有以下几个特点：
1、它是一个便于求导的连续光滑函数；
2、能够压缩数据，保证数据幅度在（0，1）之间；
3、适用于前向传播。
  但是利用Sigmoid函数作为激活函数也不得不面对以下几个问题：
1、sigmoid函数面临着梯度弥散问题(gradient vanishing)。
从图中可以看出，当输入过大时，及时很大的变化也会引起很小的输出，即梯度消失，这就是梯度弥散问题。
并且这个问题会随着网络深度的增加而增加，使网络的学习停留在一定的水平后，很难继续学习。
2、Sigmoid函数的输出不是零均值(zero-centered)或者中心化的。以$f(x) = sigmoid(wx+b)$为例。假设输入均为正数（负数），那么对w的导数总是正数（负数），这样在反向传播过程中要么都往正方向更新，要么都往负方向更新，导致有一种捆绑效果，使得收敛缓慢。
3、指数运算导致计算量的增加。

tanh函数

$$tanh(x) = \frac{e^x - e^{-x}}{e^x+e^{-x}}$$

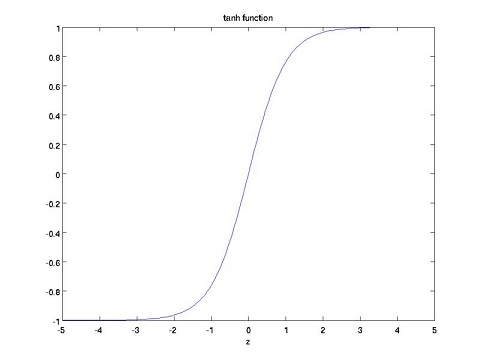
其实推导可以发现

$$tanh(x) = 2sigmoid(2x) - 1$$

  tanh函数将输出压缩到了(-1,1)之间，并且是零均值的。它解决sigmoid函数非零均值的问题；并且在0附近，tanh函数更大的导数，这意味着它将提供更好的学习速率，但是梯度弥散问题在tanh函数中依然存在。

ReLU函数

$$ReLU(x) = max(0,x)$$

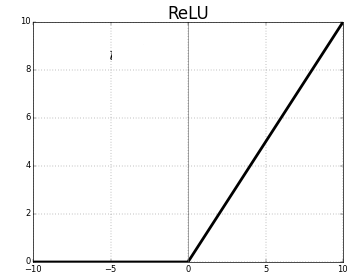
  这是在深度学习中最常用的的一种激活函数，当输入小于0时，它输出为0；当输入大于0时，它的输出为本身。因此：
1、它可以使网络更快的收敛，并且不会饱和，在正半轴解决了梯度弥散问题；
2、不需要进行指数运算，降低了计算复杂度；
3、适用于反向传播。
但是ReLU函数也有如下问题：
1、输出如sigmoid一样是非零均值的；
2、神经元坏死现象：前向传导（forward pass）过程中，如果x<0，梯度永远等于0，则神经元保持非激活状态，导致相应参数永远不会被更新。
3、不能对数据幅度做调整，因此随着网络层数的增加，数据幅度会不断地扩张。

神经网络

  神经网络是有神经元连接起来的而形成的模型，如下图：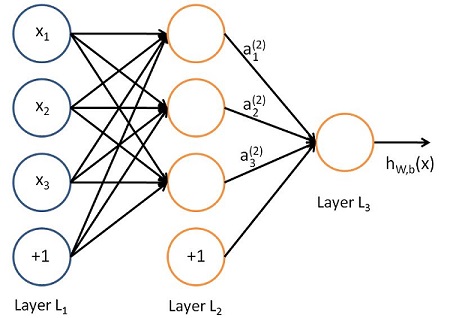

  在了解神经网络其他概念之前，有必要了解以下神经网络中Layer（层）的概念，一层Layer是指具有输入和输出的神经元，如图中的Layer2和Layer3。最左边的Layer1为网络的输入层，虽然输入层也叫层，但是在计算神经网络层数的时候，通常不计算输入层；中间的层叫做隐藏层，如上图的Layer L2； 最后一层叫做输出层，如上图的Layer L3；在计算模型层数的时候，只计算隐藏层和输出层，例如上面就是一个两层的神经网络模型。

深度神经网络

  深度神经网络一般是指具有超过一个隐藏层的模型。下面介绍一些现在常用的深度神经网络模型。

卷积神经网络（Convolution Neural Network， CNN）

  卷积神经网络是一种专门用来处理具有网格结构的数据的神经网络。例如时间序列数据和图像数据（看作二维的像素网格），现在卷积神经网络在计算机视觉领域应用非常广泛。卷积神经网络的名称来源于它使用了卷积（convolution）这种数学运算，即一种特殊的线性运算。但是卷积模型除了卷积层，还通常包含池化层，全连接层和归一化层。

卷积运算

  在卷积网络的术语中，卷积的第一个参数通常叫做输入，第二个参数叫做核函数（kernel function)， 输出常称为特征映射（Feature Map)。卷积运算的过程可以通俗的理解为一个输入经过一个“滤波器（卷积核）”产生输出（Feature Map）。
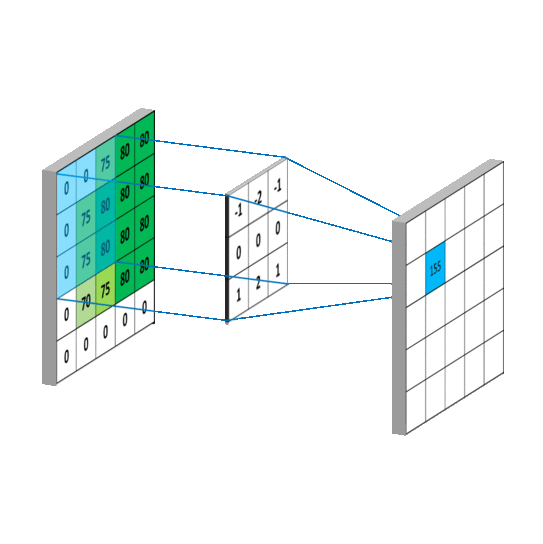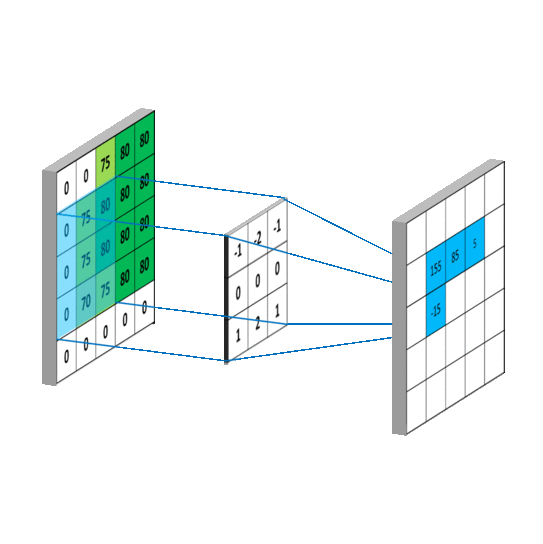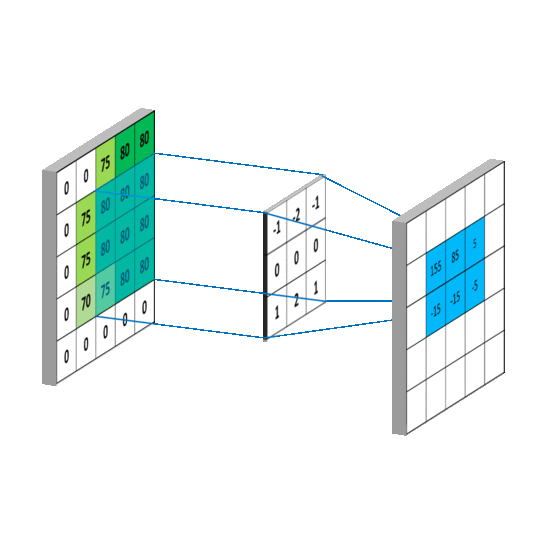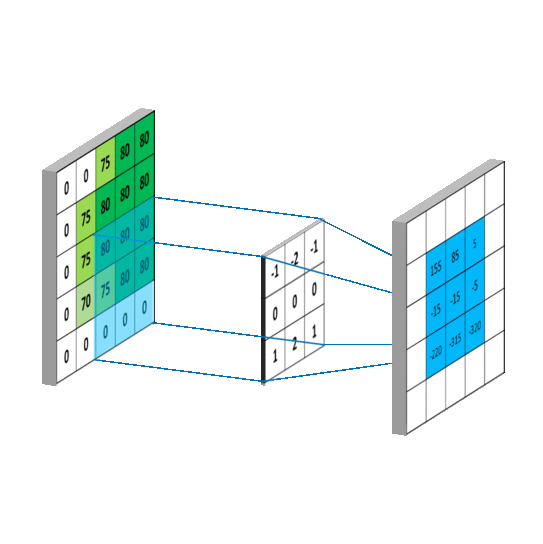
  卷积运算的计算过程如下图所示：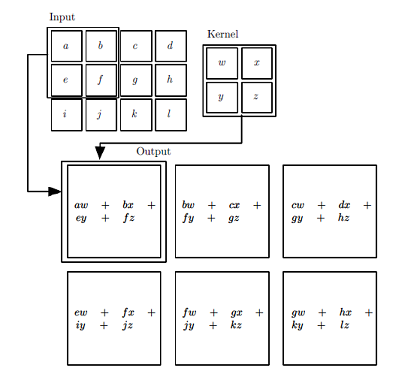

  根据上图的卷积计算过程，可以看到下图这个例子中155的计算过程：

$$0\times -1 + 0\times -2+75\times -1+0\times 0+75\times 0+80\times 0+0\times 1+75\times 2+80\times 1 = 155$$

池化(Pooling)运算

  池化是一个基于采样的离散化处理。它的目标是对输入(图片，隐藏层，输出矩阵等)进行下采样，通过去掉Feature Map中不重要的样本，进一步减少参数数量。
Pooing的方法很多，最常用的是Max Pooing，即在 $n \times n$ 的样本中取最大值作为采样后的值；对于深度为D的Feature Map，各层独立做Pooing，因此Pooing后的深度仍然为D。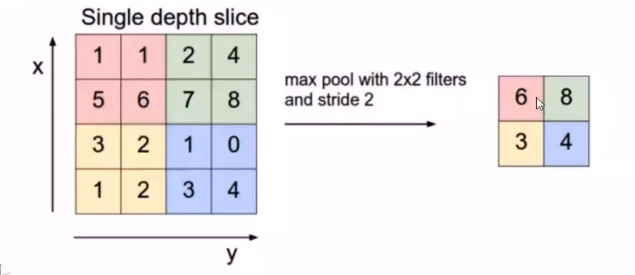

循环神经网络（Recurrent Neural Networks， RNNs）

  循环神经网络已经在众多自然语言处理(Natural Language Processing, NLP)领域中取得了巨大成功。下图展现了RNNs的结构图以及对应的展开图。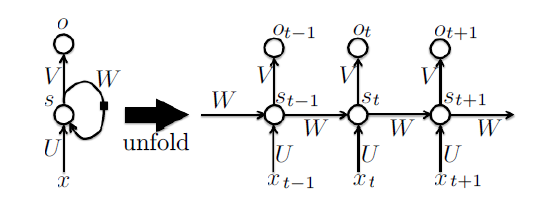

  通过这个图我们可以清晰的看到RNNs的计算过程。网络在t时刻接收到输入$x_t$之后，隐藏层的值$s_t$是，输出值是$o_t$。关键一点是，本层不仅仅取决于本层输入，还取决于上一层的输出。这个特性可以利用被用于处理语言模型中词语的关联性。在实际语言处理时，要推测当前词仅仅关注前面的词语是不够的，往往还需要后面的词，这个时候往往需要使用双向循环神经网络。